Banks in a post-LIBOR world that have been using the LIBOR/Interest Rate Swap curve as the basis for their Funds Transfer Pricing (FTP) will have to make changes to replace LIBOR as it is phased out. This may be a good time for banks using other indices like FHLB Advances and Brokered Deposits to evaluate the effectiveness of their methodologies for serving their intended purpose. In both situations, newly available interest rate index curves can provide the basis for an FTP curve designed to capture the separate elements of interest sensitivity, liquidity, and credit.
LIBOR has been the mainstay of pricing for banks for over three decades and it is the foundation for the multi-trillion-dollar interest rate derivatives market, most interbank funding transactions, and much of the pricing on deposits and commercial loans. It is also one of the primary foundational components of FTP in many banks.
The interest rate curve derived from the LIBOR/Swap curve is the interest rate component of FTP at most large banks. It usually is combined with a liquidity transfer price curve to form a composite FTP curve. Mid-sized and smaller banks often use the FHLB Advance curve which sometimes is combined with brokered deposit rates as their composite FTP curve. For all approaches, the FTP curve is intended to align with their wholesale cost of funds. Hence, in varying economic environments what FTP is communicating in terms of value created from deposit taking and lending is adjusting for variations in wholesale funding costs.
However, these alternative approaches for calculating FTP do not result in the same curve. FTP is an integral part of the decision process at many banks affecting loan and deposit pricing, business line performance evaluations, and compensation. As such, having different FTP curves among banks has clear go-to-market implications. For example, the value of core deposits—a bank’s most valuable resource—will vary materially across banks with banks that calculate higher liquidity premiums willing to pay more for these deposits. At the same time, higher liquidity charges will negatively impact lending by raising the hurdle rate on loans above peers with lower liquidity charges.
Most large banks are adopting SOFR (Secured Overnight Funding Rate) as their replacement of LIBOR for use with indexing floating rate loans and for hedging. SOFR is based on actual borrowing transactions secured by Treasury securities. It is reflective of a risk-free rate and not bank cost of funds, so a fixed compensating spread must be added to SOFR to align with LIBOR. In varying economic conditions where bank cost of funds would vary, adjusted SOFR will not reflect these changing conditions.
Many mid-tier banks are gravitating to Ameribor and Bloomberg Short-Term Bank Yield Index (BSBY)[1] which provide rates based on an aggregation of unsecured bank funding transactions, although different methodologies are used to calculate these indices. Using these indices does solve the problem of cost relevance for banks but are limited in certain cases. These indices create a combined interest sensitivity / liquidity interest rate curve which means that interest rate and liquidity implications cannot be decomposed for, say, differentiating a 3-month loan from a 5-year loan that reprices every three months.
An effective FTP measure must at least:
- Accurately reflect the interest rate environment
- Appropriately reflect a bank’s market cost of funding in varying economic markets
- Be able to separate interest rate and liquidity components for floating rate and indeterminant maturity instruments
These three principles alone set a high bar for a replacement rate for LIBOR and for how it is applied. They also highlight the challenges of using a single index for both interest rate and liquidity FTP. As described, none of the new indices—SOFR, Ameribor, and BSBY–can meet these basic FTP principles by themselves, neither can FHLB Advances or brokered deposits.
So, how to proceed. If we take a building block approach to this problem, then we want to consider what the potential building blocks are which can contribute to meeting our principles.
SOFR is intended to accurately reflect the interest rate environment and the use of Treasury-secured transactions seems to meet that objective. The addition of a fixed risk-neutral premium to SOFR provides an interest rate index like the LIBOR/Swap curve, but with much more depth of market transactions supporting the index. However, at this time recognized Term SOFR yields extend only out to twelve months. For terms beyond 12 months, an alternative similar to SOFR, like term Treasury yields, must be used.
Conversely, FHLB Advances and brokered deposits are composite curves which represent bank collateralized or insured wholesale funding costs. They capture composite interest sensitivity and liquidity but lack any form of credit risk for term funding. This works fine under some conditions, but often will put these banks at a pricing disadvantage for gathering core deposits relative to banks that value liquidity more highly.
Both Ameribor and BSBY are designed to provide a term structure of bank credit sensitive interest rates representative of bank unsecured financing costs. Effectively, these indices provide a composite FTP curve capturing interest sensitivity, liquidity, and credit sensitivity. However, because they are composite indices, interest sensitivity and liquidity cannot be decomposed and measured separately. Hence, floating rate and indeterminant-maturity transactions will be difficult to correctly value since term structure and interest sensitivity are independent.
Using some of these elements as building blocks, a fully-specify FTP curve that separately captures interest sensitivity, liquidity, and credit sensitivity can be built which meets the three FTP principles described above.
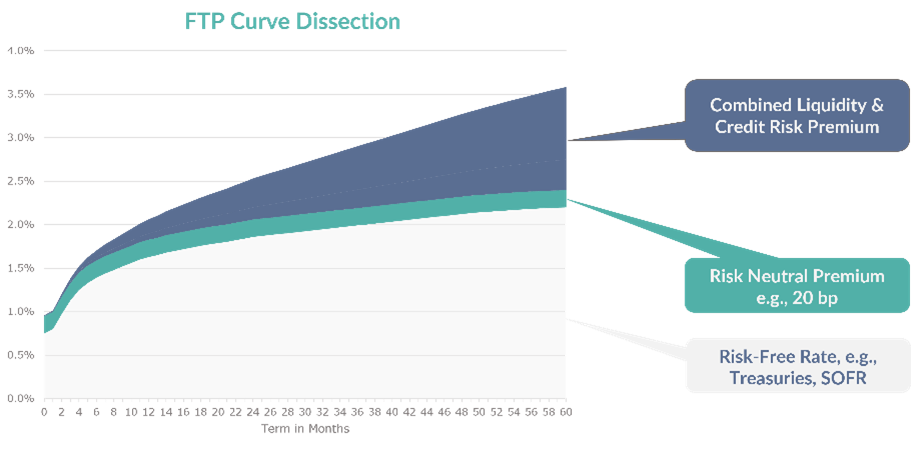
As shown in this graphic, a robust FTP curve can be created by combining SOFR, a risk-neutral premium, and Ameribor or BSBY. From these elements, an FTP measure can be created which sends appropriate signals on valuation, pricing, and performance in all interest rate and economic environments
First, SOFR establishes the foundation of the curve which is the interest sensitivity component of the FTP curve. The addition of the fixed risk-neutral premium to the SOFR curve is intended to align with what the interest rate swap curve had provided—a non-liquidity or credit-adjusted interest rate curve.
Next a measure of the all-in interest sensitivity, liquidity, and credit components of the curve can be attained from either Ameribor or BSBY. This is the upper edge of the graphic shown above. This curve alone can be used for fixed rate instruments but is insufficient for floating rate and indeterminate maturity instruments.
Finally, by subtracting the adjusted SOFR curve from the aggregate—Ameribor or BSBY—curve, a separate liquidity/credit curve (the dark blue section of the graphic above) can be created. For the purists, this section can be separated into a liquidity portion at roughly five to seven basis points per year of term and the remainder as the credit component.
This separation of interest sensitivity from liquidity/credit FTP components allows for different FTP calculations for floating rate and indeterminate maturity instruments. By using these separate elements, different FTP results can be obtained for, say, a five-year fixed rate loan, a five-year loan that reprices every three months, and a three-month loan. The phasing out of LIBOR and the introduction of alternative indices for FTP is forcing reviews of the fundamental components of FTP. As described, today banks are not using one approach to calculate FTP and the results of these different approaches have significant go-to-market implications which need to be evaluated at the most senior levels of management.
[1] BSBY (Bloomberg Short-Term Bank Yield Index) intends to represent yields on senior unsecured funding notes of large international banks published daily for overnight, 1-month, 3-month, 6-month and 12-month terms.
About Empyrean
Empyrean is a balance sheet management system for the measurement and simulation of interest rate, liquidity, credit, and capital risks faced by financial institutions. The core of the system is Empyrean ALM™ which is the most efficient and intuitive analytic, forecasting, and simulation engine on the market. Large and mid-tier banks use Empyrean ALM™ to evaluate more balance sheet strategies across more scenarios than they can on any other system.
A single cash flow engine drives Empyrean ALM™ and an array of modules which extend core capabilities. The modules support liquidity stress testing, funds transfer pricing, deposit behavioral analytics, and credit risk analysis.
Empyrean achieves extraordinary speed and efficiency through its completely modern architecture developed using the Microsoft .NET Framework, giving the user the ability to install it in a multi‐user server environment.
About Steve Turner
Steve Turner is Managing Director at Empyrean Solutions focused on introducing Empyrean ALM to the largest, most sophisticated banks in the U.S., Canada, U.K., and E.U. In this role, he leverages his experience as a successful financial services industry executive and consultant who has led engagements in treasury, liquidity management, balance sheet and capital strategies, finance, regulatory risk compliance, and credit portfolio oversight.
He regularly presents and chairs industry risk conferences and is an invited speaker at FFIEC events. He has published in numerous industry journals including Bank Director, Bank Accounting and Finance, Commercial Lending Review, and American Banker.
Prior to joining Empyrean Solutions, Steve held Managing Director positions at Novantas and First Manhattan Consulting Group. He started his career leading treasury at Shawmut National Corporation, a leading Northeast regional bank now part of Bank of America. He has an undergraduate degree in economics from Allegheny College and an MBA in finance from Tulane University.
Want to learn more?
Stay connected with Empyrean’s latest insights and solutions
Join our community of financial institutions and get access to live webinars, comprehensive guides, best practices, and industry insights that will transform your institution’s risk and planning management processes.
